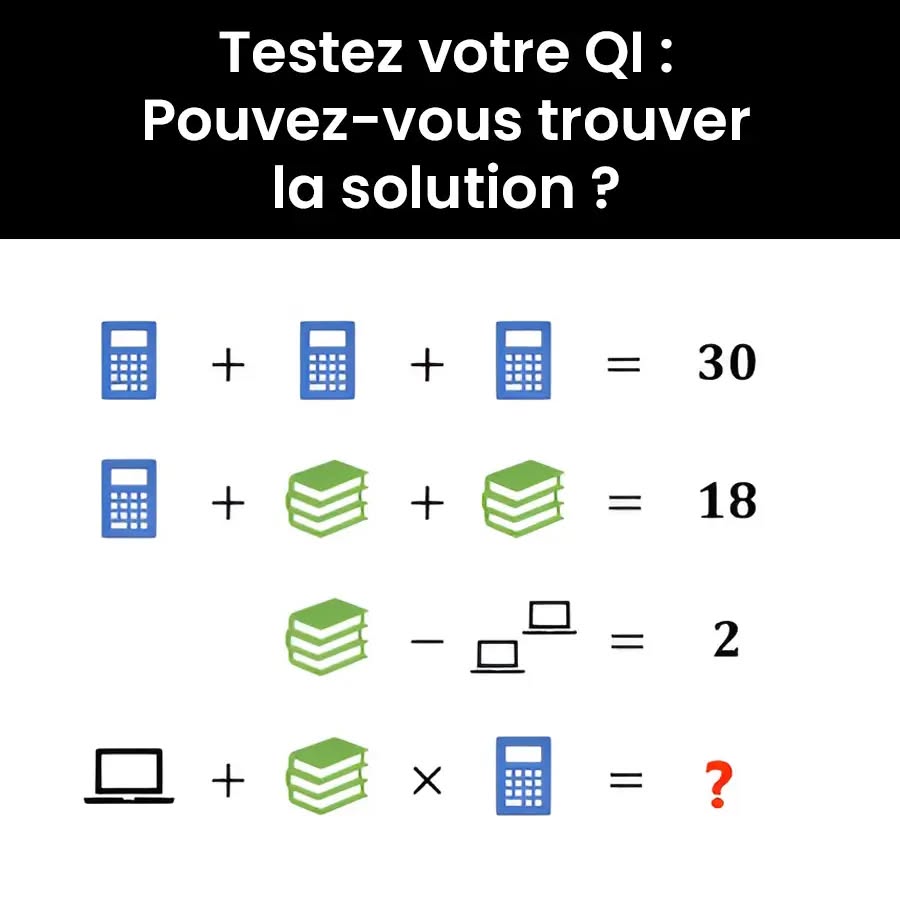
L’énigme mathématique partagée par le ministre de l’Éducation argentin a rapidement enflammé les réseaux sociaux, suscitant diverses interprétations. Découvrez pourquoi ce casse-tête en apparence simple divise tant l’opinion.
Le dilemme
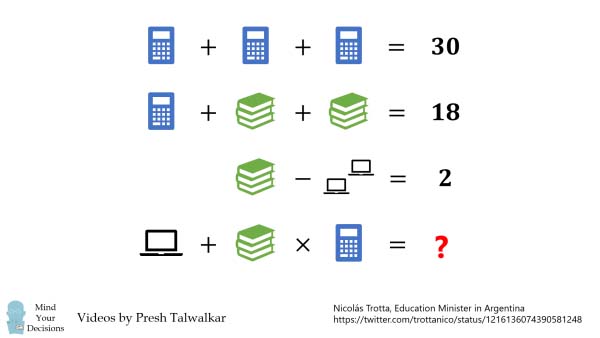
Envisagez une équation où des objets du quotidien tels que des calculatrices, des livres et des ordinateurs portables sont utilisés à la place des chiffres. Votre défi ? Déterminer la valeur de chaque objet tout en maintenant l’équilibre de l’équation. Pas si simple, n’est-ce pas ?
Ces énigmes visuelles exigent une vigilance particulière car chaque détail est crucial :
- Les symboles se ressemblent, mais ne sont pas identiques. Par exemple, un livre peut avoir un nombre de pages différent, ou une calculatrice peut afficher un écran distinct.
- Les opérations sont conventionnelles, mais la clé réside dans votre capacité d’observation minutieuse.
Résolution du dilemme
Commençons par définir les variables :
- CC représente une calculatrice,
- BB un groupe de livres,
- LL une paire d’ordinateurs portables,
- xx un unique ordinateur portable.
Les équations données sont les suivantes :
- C+C+C=30C+C+C=30
- C+B+B=18C+B+B=18
- B−L=2B−L=2
- x+B×C=?x+B×C=?
Étape 1 : Déterminons CC à partir de la première équation.
C+C+C=30C+C+C=30
3C=303C=30
C=10C=10
Étape 2 : Calculons BB en utilisant la deuxième équation.
C+B+B=18C+B+B=18
10+2B=1810+2B=18
2B=82B=8
B=4B=4
Étape 3 : Trouvons LL grâce à la troisième équation.
B−L=2B−L=2
4−L=24−L=2
L=2L=2
⏬️⏬️ Suite page suivante ⏬️⏬️
voir la suite à la page suivante
Pages : 1 2